
이진트리란 하나의 노드가 있을때, 자식노드가 2개 이하인 트리를 말한다.
자식노드가 3개라면 이진트리라 부를수 없다.
트리를 사용하는 이유는 데이터를 계층적으로 구성하며 효율적으로 관리하기 위해 사용된다.
계층적 구조를 이룸으로써 빠른 검색, 삽입, 삭제가 가능하다.
이러한 트리구조에서 모든 노드를 빠르게 확인하거나, 처리를 하기위해선 순회 방법을 알아야한다.
순회 방법으로는 전위순회 중위순회 후위순회가 있다.
전위순회 Preorder , 중위순회 Inorder , 후위순회 , Postorder
각 접두사를 확인해보면 Pre, In, Post 로 앞에 , 안에 , 뒤에 로 유추할수 있다.
단어의 각 위치는 트리의 Root의 위치를 의미한다.

위와 같은 간단한 트리가 있을때, Root는 A 로 Left는 B , Right는 C로 구성된다.
Preorder의 경우 Root가 맨앞이라는 의미는 순회의 순서에 있어 Root를 가장먼저 탐색함을 의미한다.
이후 왼쪽 , 오른쪽 순으로 탐색을 진행하게된다.
그럼 Preorder 전위 순회는 Root - Left - Right 로 A - B - C 순으로 접근하게된다.
Inorder 중위 순회는 Root의 순회순서를 중간에 넣음으로 Left - Root - Right 로 B - A - C 가 된다.
Postorder 후위 순회 Root의 순회순서를 맨뒤에 넣어 Left - Right - Root 로 B - C - A 가 된다.

다시 이 트리로 넘어와 각 순회를 해보자.
전위순회 ROOT - LEFT - RIGHT
A부터 시작으로 자식노드를 확인한다.

위와 같은 트리를 확인할수 있다. 이때 루트인 A먼저 확인하면 된다.
다음은 왼쪽인 B에 접근하게 된다.
B의 노드를 확인해보면

B에 대한 트리 정보를 확인할수 있다.
이때 루트인 B를 확인하면 된다. 다음 왼쪽인 D를 확인해보면
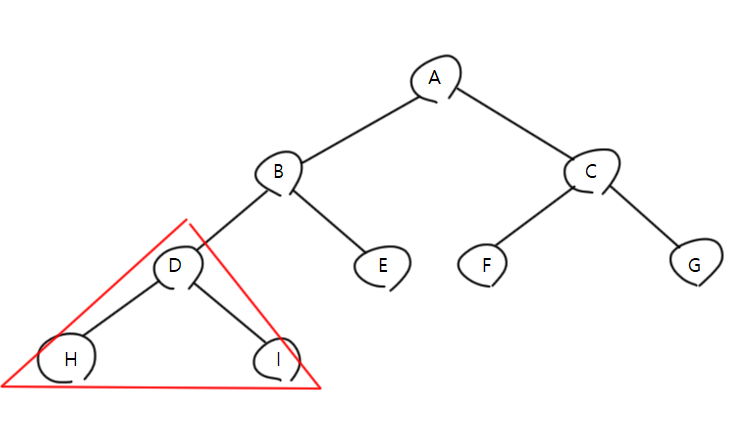
루트인 D를 찍어주면 되고 H에 접근해보면
H는 왼쪽도, 오른쪽도 없다.
다시 D 노드로 돌아와 왼쪽자식 H는 순회를 마쳤으므로 오른쪽자식 I를 순회를 해보면
마찬가지로 I 의 자식들은 없다. I 트리의 루트인 자신을 확인한다.
여기까지의 순서는 A - B - D - H - I 로 해당 D트리에 대한 순회가 끝났으므로 이전의 B 트리로 되돌아 간다.

B 트리의 왼쪽자식 D의 순회는 끝났고 다음 자식인 E 노드를 확인한다.
E 노드의 자식은 없으므로 루트인 자신을 확인하고 되돌아간다.
B 트리에 대한 순회가 끝났다.
기존 A 트리의 순회로 되돌아간다.

A 트리의 왼쪽 순회는 끝났고, 오른쪽 자식 C 에 대해 접근한다.
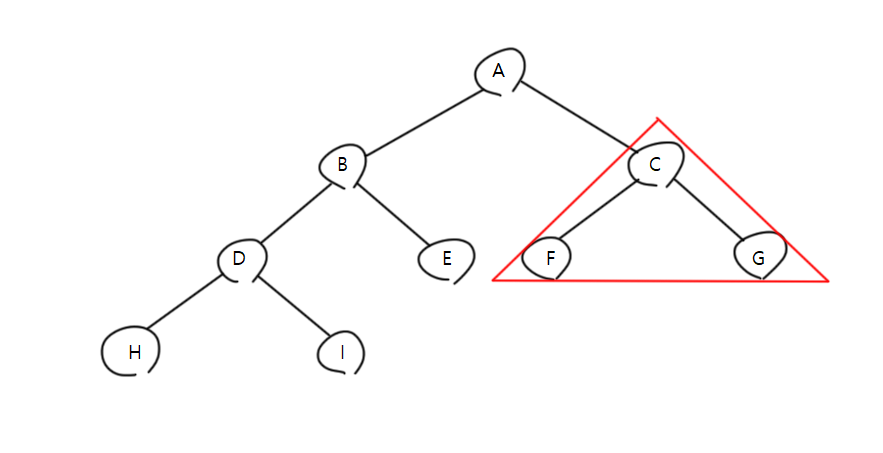
C 트리에서 왼쪽 F - G 를 확인한뒤 다시 되돌아간다.

이로써 A 트리의 전위 순회 Root - Left - Right 순회를 마친다.
A - B - D - H - I - E - C - F - G
중위순회 LEFT - ROOT - RIGHT

A 부터 접근을 시작한다.
A트리의 왼쪽 B에 대해 접근한다.

B 트리에 접근한뒤 왼쪽자식 D에 확인한다.

D 트리에 접근한뒤 왼쪽 자식 H를 확인한다.
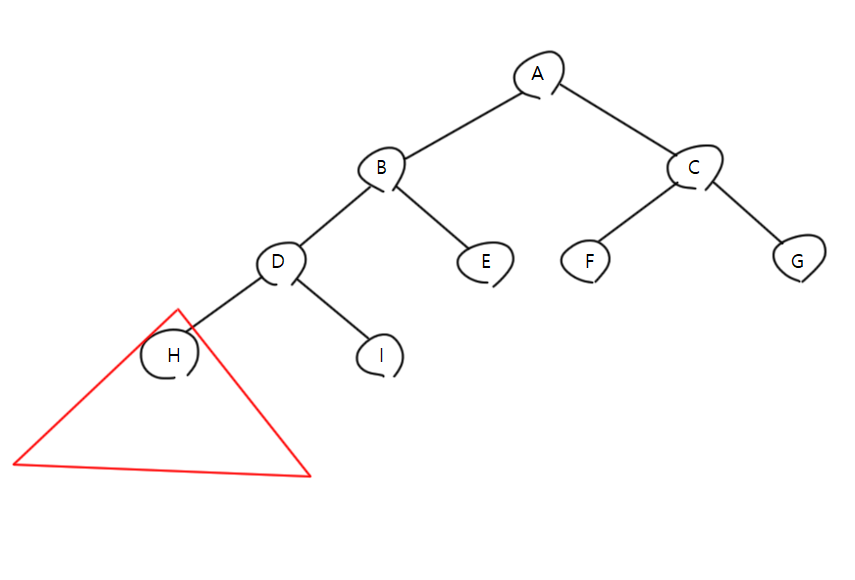
H 트리에서 더이상 순회할것이 없다.
순서인 LEFT(없음) - ROOT(H) - RIGHT(없음) 으로
H 를 확인한뒤에 다시 D 트리로 되돌아간다.

D 트리의 왼쪽 H의 확인이 끝났으므로 루트인 자신을 확인한다. H - D
이후 오른쪽 I에 대해 확인하지만 H와 마찬가지로 순회를 해준다.
다시 D 트리로 되돌아와 해당 트리의 순회로 현재 H - D - I 순회를 거쳤다.
다시 B 트리로 되돌아간다.

B 트리의 왼쪽 D 트리의 순회가 끝났으므로 루트인 자신을 확인. H - D - I - B
이후 오른쪽 E 를 확인. H - D - I - B - E
B 트리 순회 끝으로 A 트리로 되돌아간다.

A 트리의 왼쪽 B 노드의 순회가 끝났으므로 루트 자신을 확인 H - D - I - B - E - A
오른쪽 C에 대해 접근

C 트리의 순회로 F - C - G 순회가 종료된다.

H - D - I - B - E - A - F - C - G
후위순회 LEFT - RIGHT - ROOT

A 트리에서 B 로 접근

B 에서 D 로 접근

D 에서 H 로 접근

Left(없음) - Right(없음) - Root(H)로 H를 확인
다시 D트리로 이동

왼쪽 순회가 끝나고 오른쪽 순회 I
I 에 대해 더이상 노드가 없으므로 I 를 확인 H - I
다음 D 트리에 대해 순회순서 왼쪽과 오른쪽순회가 끝났으므로 Root 인 자신을 확인 H - I - D
B 트리로 되돌아간다.

B 트리의 왼쪽 순회 완료
오른쪽 E 순회로 H - I - D - E
다음으로 루트인 B를 확인 H - I - D - E - B
다시 A 트리로 이동

A 트리의 왼쪽 순회 완료
오른쪽인 C 노드에 접근

C 트리에서 순회 F - G - C 이후 다시 A 트리로 되돌아간다. H - I - D - E - B - F - G - C

A트리의 왼쪽과 오른쪽을 모두 순회 했으므로 루트인 자신을 확인
H - I - D - E - B - F - G - C - A
'알고리즘 > 탐색' 카테고리의 다른 글
| 브루트포스 알고리즘 - Brute Force (0) | 2024.11.10 |
|---|---|
| 백트레킹? BackTracking (2) | 2024.02.28 |
| 이진 탐색 (0) | 2024.02.22 |