백트레킹은 시도와 오류 방식을 기반으로
모든 방법을 시도하되, 현재의 경로가 해결책으로 이어질 가능성이 없다고 판단될때
이전의 분기점으로 되돌아가 다른경로를 시도하는 방식이다.
최적화 문제, 조합문제를 해결하는데 유용할수 있다.
예시의 경우를 살펴보자

위와같은 노드가 있고 노드의 리프에 도착했을때
모든 노드의 합이 6 이 되는 경로를 찾아야된다고 할경우를 가정해보자.
DFS 방식으로 탐색을 진행할경우
왼쪽방향으로 먼저 탐색하게 될것이다.

위처럼 리프에 도달했을때 노드의 총합은 21이라는 틀린값이 나오게된다.
하지만 이때 백트레킹 기법을 활용하게 된다면

노드 중간에 이미 찾아야하는 값이 먼저 나와버렸고, 해당 정점이 리프가아니므로 더이상 탐색은 의미가 없게되어버린다.
이때 다시 부모 분기점으로 되돌아가 다른 탐색을 진행한다.

이처럼 백트레킹 기법을 활용으로 불필요한 탐색과 반복문을 효과적으로 줄일수 있게된다.
하지만 해당 기법을 효율적으로 활용하기 위해선 조건을 얼마나 잘 걸어주느냐에 따라 코드의 효율이 결정될것이다.
문제 https://www.acmicpc.net/problem/9663
9663번: N-Queen
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
풀이
int n = int.Parse(Console.ReadLine());
int count = 0;
int[] board = new int[n];
Array.Fill(board,-1);
for (int i = 0; i < n; i++)
{
DFS(i,0);
}
System.Console.WriteLine(count);
void DFS(int column,int step)
{
for (int j = 1; j < step + 1; j++)
{
int critical_left = column - j;
int critical_right = column + j;
if (board[step - j] == critical_left ||
board[step - j] == critical_right)
return;
}
if (step >= n-1)
{
count++;
return;
}
board[step] = column;
for (int i = 0; i < n; i++)
{
if(column-2 < i && i < column+2)
continue;
if(board.Contains(i))
continue;
DFS(i,step+1);
board[step+1] = -1;
}
}
해당 문제 풀이방식

맨 윗줄을 시작으로 맨 아랫줄까지 배치가 완료되면 Count를 증가시키는 방식을 생각했다.
모든 경우를 확인하기위해 for( 0번째칸부터 , N까지 ) { DFS() } 방식으로 재귀함수를 활용했다.
1차원배열이나 2차원배열을 사용하여 문제를 풀며 기저조건을 만나게되면
체스판의 상태를 다시 되돌려둬야한다.
이때 배열을 다시 복사하는 형태로 진행했더니 메모리 초과가 발생했다.
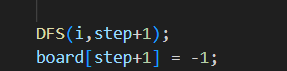
원래의 상태로 되돌리기 위해 다음 재귀를 돌리기전
다시 원래 상태로 복구시키는 방식을 사용함으로써 배열 하나로 문제를 해결할수있게 되었다.
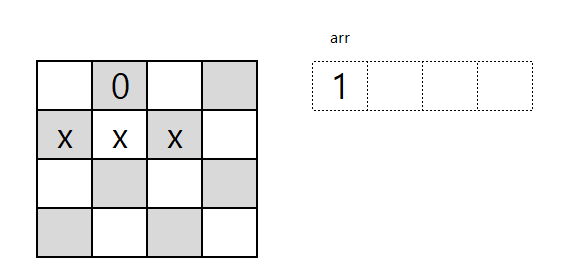
위 그림처럼 2번째 줄에 말을 배치해야할때
이전줄의 말의 대각왼쪽 , 아래 , 대각오른쪽은 배치를 할수 없으므로
해당 조건을 줌으로써 반복문을 조금더 줄여보려 했다.
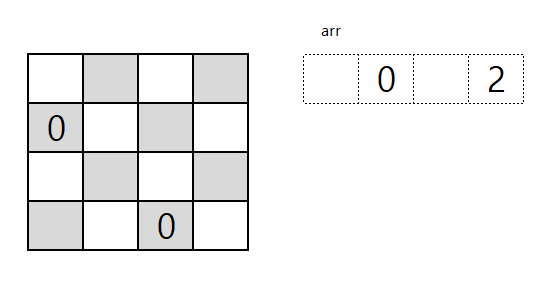
대각선으로 겹쳐지게 되는 경우인데,
말을 하나 둘때 대각 4방향을 전부 확인하지 않고 대각왼쪽, 대각오른쪽만 확인을 진행하며
겹쳐지는 말이 있다면이라는 기저조건을 넣어주었다.
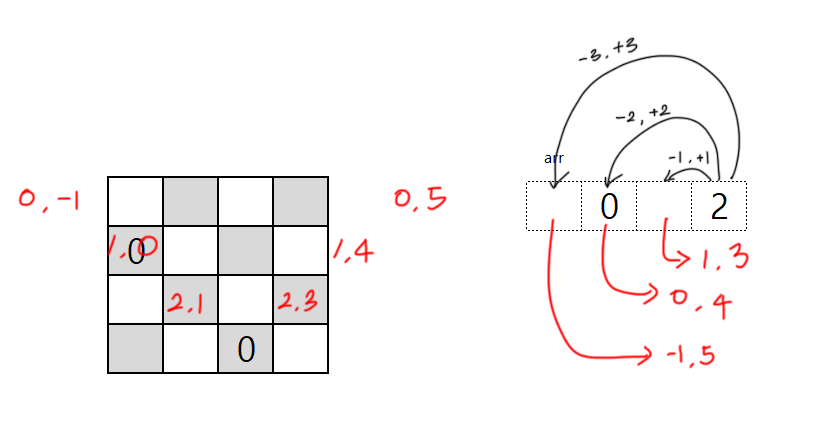
대각왼쪽, 대각오른쪽을 전부 확인했던 방법은
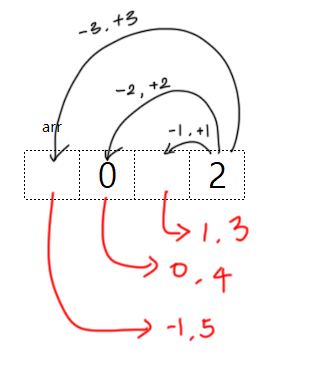
해당하는 배열순번에 있으면 안되는 번호가 있다면 해당탐색을 취소시키는 방법으로 진행했다.
미흡한부분이나 개선될 수 있는부분이 있다면 댓글 부탁드립니다.
'알고리즘 > 탐색' 카테고리의 다른 글
| 브루트포스 알고리즘 - Brute Force (0) | 2024.11.10 |
|---|---|
| 이진트리 전위 , 중위 , 후위 순회 (2) | 2024.03.06 |
| 이진 탐색 (0) | 2024.02.22 |