kark's

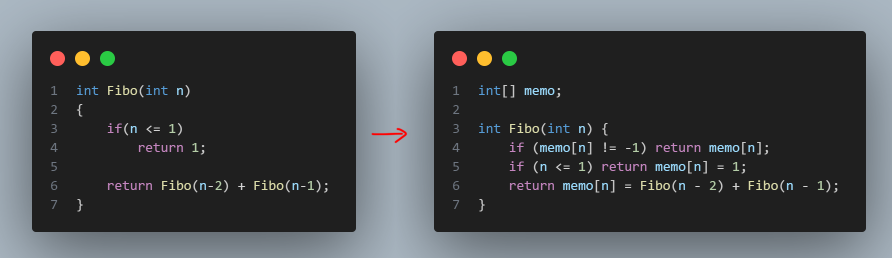
동적 계획법은 복잡한 문제를 여러개의 간단한 문제로 분리해 부분문제를 해결함으로 복잡한 문제의 답을 구하는 방법을 의미한다. 핵심 이론은 ① 큰 문제를 작은 문제로 나눈다. ② 작은 문제들이 반복되고, 작은문제들의 결과값은 항상 같아야한다. ③ 모든 작은문제는 한번만 계산돼 DP 테이블에 저장한 뒤 재사용할때는 이 테이블을 이용한다 동적계획법에는 두가지 방식 탑다운 방식과 , 바텀업 방식으로 나눠진다. 탑다운 문제를 파악하고 점차 내려오는 방식으로, 주로 재귀함수 형태로 코드를 구현한다. 이 방식은 코드의 가독성이 좋고, 이해하기 편한 장점이 있다. int[] memo; int Fibo(int n) { if (memo[n] != -1) return memo[n]; if (n

메모이제이션은 동적 프로그래밍 기법의 일환으로, 이전에 계산된 결과를 저장해두고 필요할때 재사용해 중복 계산을 피하는 최적화 방법이다. 예로, 재귀적으로 피보나치의 수를 구할때 같은값을 여러번 계산하는 것을 메모이제이션으로 방지할수 있다. 기본 재귀함수의 경우 어떠한값이 필요할때 비효율적인 중복되는 계산을 여러번 처리해야한다. 메모이제이션 기법을 사용함으로써 한번 계산된결과를 저장해둔 뒤에 똑같은 계산결과가 필요할때 계산과정을 거치지 않고 필요한 값을 바로 불러오는 방법이다. 이처럼 눈에 보이는 장점과 단점이 있는데, 장점이라면 피보나치의 수처럼 계산 비용이 높은 경우 프로그래밍의 성능을 개선시킬수 있다는점 단점이라면 추가적인 메모리가 필요한점이다. 사용해야하는경우는 비용과 이익을 고려해봐야 하겠지만 보..

함수 안에서 자기 자신의 함수를 호출되는 형태를 의미 재귀를 사용함으로 복잡한 문제를 간단하게 해결할수 있다. 재귀함수는 반복적인 작업을 수행할때 반복문을 사용하는 대신 자기 자신을 호출해 문제를 해결한다. 재귀 함수는 보통 2개의 단계로 구성된다. ① 기저조건 재귀호출을 멈추는 조건을 의미 이 조건이 없다면 함수는 무한하게 호출되므로 프로그램이 정상적으로 작동되지 않는다. ② 재귀단계 자기 자신을 호출하는 부분이다. 이구간을 통해 문제의 규모를 줄여가며, 최종적으로 ① 기저조건을 만나 재귀 호출이 종료되게된다. 장점 복잡한 문제를 간결한 코드로 작성할수 있으며 반복문보다 좀더 직관적일수도 있다. 단점 호출이 많아지면 스택 오버플로우가 발생될수있음 깊은 재귀의 경우 스택 메모리사용량이 증가된다. 시각화와..

탐욕법으로 매순간 주어지는 상황에 가장 답이 될것같은 해를 선택하는 방식의 알고리즘 수행과정 ① 현재 상태에서 가장 좋은 해를 선택 ② 선택된 해가 문제의 조건에 벗어나진 않는지 확인 ③ 현재까지의 선택한 해(집합) 이 전체적인 문제를 해결할수 있는지 확인하며, 해결되지 않을것같다면 ① 로 다시 되돌아간다. 위의 표처럼 각 화폐로 800원을 만들되, 가장 적은 수량의 화폐로 800원을 만들어야한다라고 가정해보자. 가장 큰 단위의 화폐부터 확인해보면, 800원을 만들수있는 가장큰 단위의 화폐는 500원으로 확인된다. 그리디한 방식으로 바로 500원을 선택해준다. 이후 만들어야 하는 금액은 300원으로 500원으로는 300원을 초과하기에 적합하지 않다. 다음으로 큰화폐를 조회하며 탐색을 이어간다. 문제 ht..