신장 트리는 그래프 내 모든 정점을 거치며 사이클이 없는 트리다.
N개의 정점이 있다면 간선의 수는 N-1 로 구성된다.
최소 신장트리란 각 간선의 비용을 최소화하여 구성된 모든 정점을 거치는 트리이다.
이번 글은 크루스칼(Kruskal) 알고리즘으로 해결한다.
크루스칼 알고리즘은 MST를 해결하기 위한 방법중 하나이며,
크루스칼 알고리즘 방식으로 문제를 접근하기 위해서는 유니온 파인드 자료구조를 활용해야한다.
크루스칼 알고리즘은 모든 간선의 가중치를 오름차순으로 정렬하여 순서대로 간선을 선택하며
트리를 추가하는 방식으로 작동한다.
이 알고리즘의 효율성은 간선을 정렬하는 과정과, 사이클을 형성하는지 검사하는 과정에 크게 의존된다.
간선정렬 O(E log E)
유니온-파인드 사이클형성 검사는 거의 상수시간복잡도로 구성된다.
즉, 크루스칼 알고리즘은 간선의 가중치를 정렬하는데 결정되므로 O(E log E) 시간복잡도 이거나,
간선의 수가 정점의 수보다 적을경우 O(E log V)로 표현된다.
서로소집합 DisjointSet
각 원소가 집합을 이루게 하거나, 집합을 관리하기 위해 사용되는 자료구조 각 원소가 어떤 집합에 속하는지 빠르게 찾아내고 두개의 집합을 하나로 합치는 연산을 지원한다. 최소 신장트리 알
kark.tistory.com

위와 같은 그래프가 있을때, 모든 정점을 간선으로 연결했을때 나오는 최소 간선 가중치의 합을 구하는 예시이다.

필요한 자료구조는 가장 적은값을 먼저 탐색하기위해 우선순위 큐를 사용한다.
이때 가중치를 기준으로 데이터를 반환하되, 사이클 구조발생을 방지하기위해 DisjointSet을 활용한다.
Set을 먼저 초기화해주고, 모든 간선에 대한 정보를 넣어준다.

이후 우선순위 큐에서 데이터를 뽑은뒤
4 와 5의 대표 원소값(기존에 집합이 있었는지) 확인해준다.
4 와 5의 대표 원소값은 현재 서로 다르므로 해당 경로를 채택한뒤, 하나의 집합으로 취급한다.

다음 경로는 1 - 3 을 확인한다.
Set에서 각 대표원소는 다르므로 해당경로를 채택하고, 하나의 집합으로 묶어준다.

다음 경로는 2 - 4 를 확인
Set에서 서로 다름 경로 채택, 하나의 집합으로 묶기

다음 경로는 2 - 5 를 확인
각 원소를 Find 로 탐색해보면, 2 - 2 를 나타내고 5 - 4를 나태내고, 다시 4는 2를 가리키고있다.
집합으로 묶기전에 대표원소가 같다는것은 사이클이 발생한다는 것을 의미한다.

해당 경로는 채택하지 않고 다음 탐색을 진행한다.
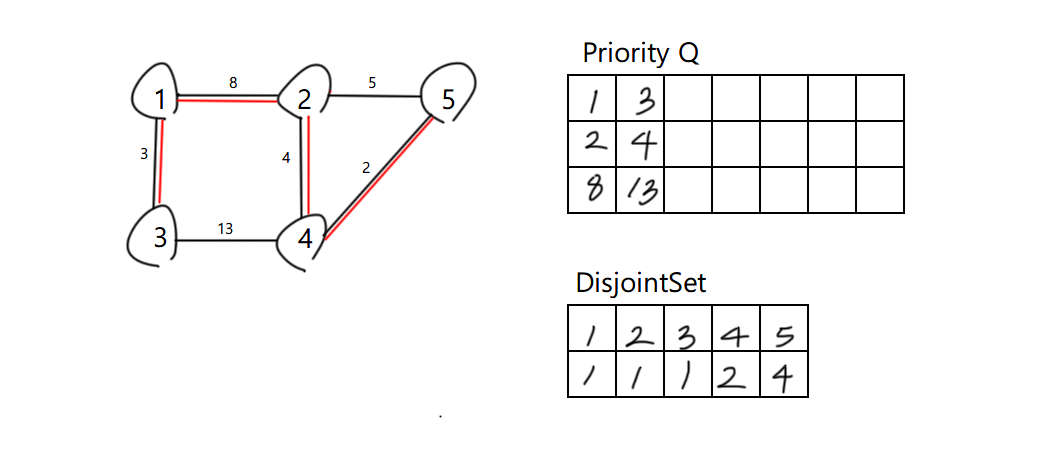
다음 경로는 1 - 2를 확인
기존의 대표원소가 달랐으므로 해당경로를 채택한다.
간선의 갯수가 V-1개로 결과가 나옴.
각 경로의 합 2+3+4+8 = 17
문제 https://www.acmicpc.net/problem/1197
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
풀이
int[] input = Array.ConvertAll(Console.ReadLine().Split(' '),int.Parse);
int v = input[0];
int e = input[1];
DisjointSet set = new DisjointSet();
PriorityQueue<(int,int,long),long> pq = new PriorityQueue<(int,int, long), long>();
for (int i = 1; i <= v; i++)
{
set.Add(i);
}
for (int i = 0; i < e; i++)
{
input = Array.ConvertAll(Console.ReadLine().Split(' '),int.Parse);
pq.Enqueue((input[0],input[1],input[2]),input[2]);
}
long sum = 0;
int step = 0;
while (true)
{
if(pq.Count <= 0 || step > v-1)
break;
(int,int,long) temp = pq.Dequeue();
int node = temp.Item1;
int target = temp.Item2;
long cost = temp.Item3;
if(set.Find(node) == set.Find(target))
continue;
set.Union(node,target);
sum += cost;
step++;
}
System.Console.WriteLine(sum);
class DisjointSet
{
Dictionary<int,int> dic;
public DisjointSet()
{
dic = new Dictionary<int, int>();
}
public void Add(int element)
{
if(!dic.ContainsKey(element))
dic.Add(element,element);
}
public void Union(int x, int y)
{
if(!dic.ContainsKey(x))
return;
if(!dic.ContainsKey(y))
return;
x = Find(x);
y = Find(y);
int min = Math.Min(x,y);
int max = Math.Max(x,y);
dic[max] = min;
}
public int Find(int element)
{
if(!dic.ContainsKey(element))
return int.MaxValue;
if(dic[element] != element)
dic[element] = Find(dic[element]);
return dic[element];
}
}
미흡한 부분이나 개선될수 있는 부분이 있으면 답글남겨주세요
'알고리즘 > 그래프' 카테고리의 다른 글
| MST 최소신장트리 - 프림 알고리즘 (0) | 2024.03.03 |
|---|---|
| Union - Find (0) | 2024.03.02 |
| Dijkstra 다익스트라 (0) | 2024.03.02 |
| DFS 깊이우선탐색 (0) | 2024.02.27 |
| BFS 너비우선탐색 (0) | 2024.02.26 |