다익스트라 알고리즘은 그래프에서 한정점에서 다른 정점으로의 최단경로를 찾는 알고리즘
edge 의 가중치가 양수여야지만 사용할수 있다.
시작 정점에서 가장 가까운(비용이 적은) 정점을 찾고, 다음으로 가까운 정점을 찾아가는 과정을 반복
① 초기 시작으로 주어진 정점의 비용을 0으로 설정하고,
나머지 정점은 아직 확인하지 못했으므로 무한대의 값으로 지정해둔다.
② 현재 정점에서 인접정점으로 가는 비용과 현재까지의 비용의 합이
인접정점이 갖고있던 비용보다 적다면 해당 비용을 수정하고 다음 탐색목록에 추가시켜준다.
이때 이미 방문했던 정점이라면 비용 수정 과정만 거치고 해당정점의 탐색은 하지 않게한다.
③ ②의 과정을 반복하며 우선순위 큐의 탐색목록이 없을때까지 또는 모든 정점의 방문이 끝났다면
탐색 완료

1을 시작으로 탐색을 진행해야한다.
1정점이 시작이므로 1정점은 이미 방문을 해뒀고, 현재까지의 거리는 0이다.
1의 인접점 2, 3 이 확인되는데 이때
2 와 3 각 정점으로 가는 비용을 확인하고 확인된 비용이 기존의 비용보다 작다면 갱신한다.
그리고 2 와 3 은 아직 방문하지 않은 정점이므로 우선순위 큐에 넣어준다.
우선순위 큐의 우선순위는 edge의 비용이 낮은 순이 우선순위가 높게한다.

가장 비용이 적은 위치로 이동한뒤, 해당 노드 3 에 방문했음을 알린다.
이후 과정을 반복하면 된다.
3의 인접점은 4
4에 도달하는데 기존비용은 무한대 값이였고
현재 위치로 오는 최소비용 3 + 다음 정점으로 가는 비용 13 = 16
새로 확인된 비용이 더 적으므로 4로 이동하는 최소비용을 수정해준다.
그리고 4 정점은 아직 방문하지 않음을 확인한뒤 우선순위 큐에 넣어준다.

우선순위큐에 다음 탐색목록 3 > 4 을 넣어주었지만,
기존 1 > 2의 비용이 더 적은값이므로 1 > 2 의 탐색 진행을 먼저해준다.

2의 인접점 확인 4, 5
현재 정점에서의 비용 8 + 각 정점에 도달하는 비용을 갱신시켜주고
인접점이 아직 방문하지 않았다면 큐에 넣어 다음 탐색으로 진행시켜준다.
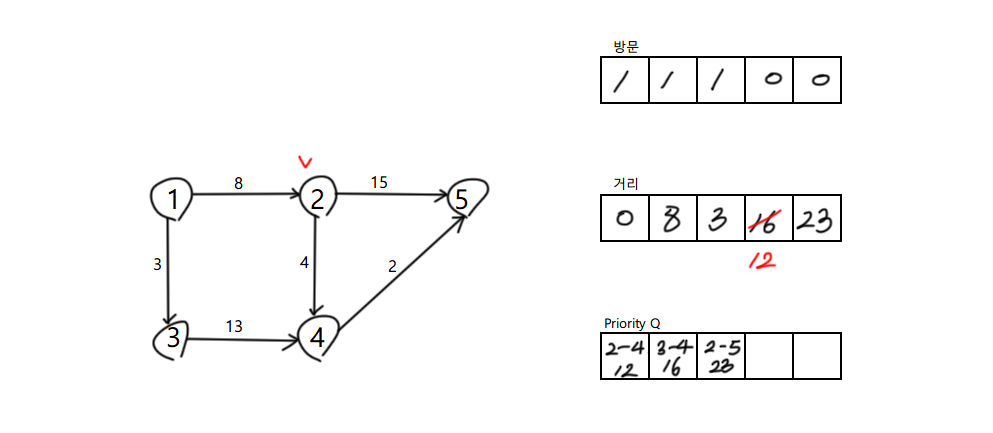
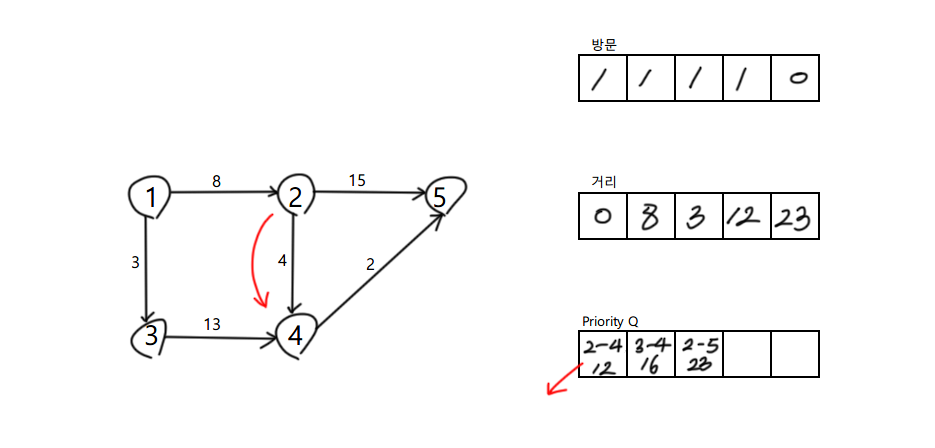
4 정점의 인접점 5
5 정점으로 가는 기존 최소비용은 23
현재 위치에서 5로 가는 비용 12 + 2 = 14 로 갱신
방문하지 않았으므로 다음 탐색에 추가
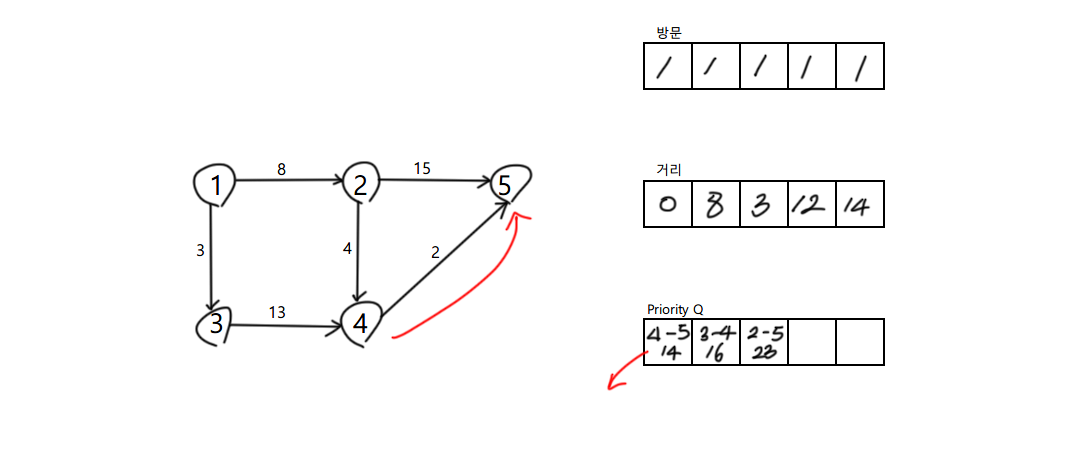
모든 노드가 방문되었고 1의 정점에서 각 정점으로 가는 모든 최소비용이 확인됨
이후 진행되는 탐색은 더이상 최소값 갱신이 없으며, 더이상 탐색추가도 일어나지 않게된다.
진행종료는 각 상황에 맞게 작성해주면 되겠다.
문제 https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
풀이
using System.Collections.Generic;
using System.Text;
int[] input = Array.ConvertAll(Console.ReadLine().Split(' '),int.Parse);
int start = int.Parse(Console.ReadLine());
int vertexes = input[0];
int edges = input[1];
PriorityQueue<(int,int),int> pq = new PriorityQueue<(int,int),int>();
Dictionary<int,List<(int,int)>> nodesInfo = new Dictionary<int, List<(int, int)>>();
int[] costs = new int[vertexes+1];
int[] visited = new int[vertexes+1];
Array.Fill(costs,int.MaxValue);
costs[start] = 0;
for (int i = 0; i < edges; i++)
{
input = Array.ConvertAll(Console.ReadLine().Split(' '),int.Parse);
if(!nodesInfo.ContainsKey(input[0]))
nodesInfo.Add(input[0],new List<(int,int)>());
nodesInfo[input[0]].Add((input[1],input[2]));
}
pq.Enqueue((start,0),0);
while (true)
{
if(pq.Count <= 0)
break;
(int,int) temp = pq.Dequeue();
int cur_v = temp.Item1;
int cur_cost = temp.Item2;
if(visited[cur_v] == 1)
continue;
visited[cur_v] = 1;
if(!nodesInfo.ContainsKey(cur_v))
continue;
for (int i = 0; i < nodesInfo[cur_v].Count; i++)
{
(int,int) edge = nodesInfo[cur_v][i];
int next = edge.Item1;
int edgeCost = edge.Item2;
if(cur_cost + edgeCost < costs[next])
{
costs[next] = cur_cost + edgeCost;
if(visited[next] == 0)
pq.Enqueue((next,costs[next]),costs[next]);
}
}
}
StringBuilder sb = new StringBuilder();
for (int i = 1; i <= vertexes; i++)
{
if(costs[i] != int.MaxValue)
sb.AppendLine($"{costs[i]}");
else
sb.AppendLine("INF");
}
System.Console.WriteLine(sb);'알고리즘 > 그래프' 카테고리의 다른 글
| MST 최소신장트리 - 프림 알고리즘 (0) | 2024.03.03 |
|---|---|
| MST 최소신장트리 - 크루스칼 알고리즘 (0) | 2024.03.02 |
| Union - Find (0) | 2024.03.02 |
| DFS 깊이우선탐색 (0) | 2024.02.27 |
| BFS 너비우선탐색 (0) | 2024.02.26 |