가장 긴 증가하는 부분 수열 2 - 이진탐색

문제 https://www.acmicpc.net/problem/12015

12015번: 가장 긴 증가하는 부분 수열 2

 

 

조건

수열의 크기 1 <= 1,000,000

각 요소의 값 1 <= 1,000,000

 

DP 방식으로 문제를 해결했던 LIS 1번 문제와는 달리 수열의 크기가 엄청 커졌다.

 

DP 방식으로 2번 문제를 해결하고자 한다면,

N 번째 요소에서 가장 긴 수열을 찾기위해 0 ~ N-1 순회를 해야하므로 시간복잡도는 O(N²)

 

(1,000,000)² = 1,000,000,000,000

해당 문제 풀이의 제한시간은 1초

1초에 대략 1억번의 연산이 가능할때, 배열의 크기가 최대치일때 1조 번의 연산이 필요하므로

DP 방식으로 문제를 접근하면 시간초과가 발생한다.

 

이 문제를 해결하기 위해선 O(N²) 미만방식으로 접근해야한다.

N 번 요소에서 가장 긴 수열을 찾기위해 0~N-1 의 N-1 / 2씩 줄이며 순회하면 어떻게될까

O(NlogN) 시간복잡도로 1,000,000 x 20 = 20,000,000 으로 시간제한인 1초이하로 문제를 해결할수 있다.

 

순회의 횟수를 줄이는 방법으로는 이진탐색이 있다.

이진탐색은 정렬된 배열을 순회할경우 O(logN) 의 시간복잡도를 나타낸다.

 

예제로 사용할 배열이다.

 

배열의 요소의 전체순회는 필수적이다.

배열을 순회하며 선택한 요소의 앞의 요소를 전부 순회할수는 없고, 이진탐색으로 접근하는 방식을 사용한다.

 

이진탐색의 조건으로는 정렬된 배열이 있어야한다.

하지만 주어진 배열은 정렬이 되어있지 않으므로 주어지는 배열로 이진탐색을 할수가 없고,

새로운 배열이 필요하다.

 

모든 요소를 순회했을때 만들어지는 수열의 크기는 아직 모르니 리스트로 만들어준다.

 

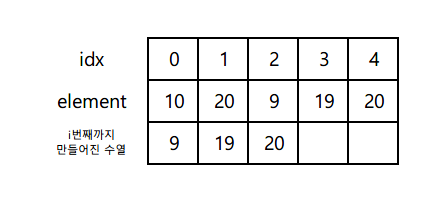
위의 표처럼 요소가 하나일때,

가장 긴 부분수열은 10 하나로 구성된다.

 

리스트를 사용해 마지막에 만들어질 가장 긴수열을 직접 만드는 방법을 사용한다.

다음요소 20

현재 리스트에 마지막요소인 10 보다 크므로 이어지는 수열로 판단이 된다. (10 - 20)

리스트에 추가시켜주면 되겠다.

다음 요소 9

리스트의 마지막 요소와 비교해보지만 해당값이 더 작으므로

리스트에 추가시켜주면 안될것같다. 

 

하지만 해당 문제의 답은 3으로 (9 - 19 - 20) 또는 (10 - 19 - 20) 으로 이루어져야한다.

 

9를 버리게되면 안될것같고, 이후에 나오는 19 또한 다른 방법으로 처리해줘야한다.

각 숫자를 리스트의 알맞는 위치에 교체했을때와 교체하지 않았을때를 확인해보자.

교체할경우                                                                                                     교체하지 않을경우

 

교체하지 않을경우 다음으로 받아와야할 20을 받지 못하게 된다.

 

위 그림처럼, 가장 긴 부분수열의 마지막 요소보다 작은경우 해당요소를 기존 부분수열내에서

위치시키는 이유는 더 긴 부분수열을 만들수 있는 가능성을 두기 위함이다.

 

교체를 시킨다는 전제하에 다시 돌아와서 9를 맞는 위치에 위치시켜줘야한다.

알맞는 위치는 i 번째 요소 보다는 작은곳에 둬야한다.

 

만약 9가 아닌, 11이였다면 20을 11로 교체해주면된다. (10 - 11) 수열이 만들어지게

 

그리고 알맞는 위치를 찾을때 앞에서부터 하나씩 순회하게 되면 시간초과가 발생되므로

이상황에서 이진탐색을 진행해야한다.

 

이진탐색을 모르는 경우 https://kark.tistory.com/8

이진 탐색

 

 

위의 과정을 반복해 리스트를 완성시켜주면 가장 긴 부분수열이 완성된다.

풀이

Console.ReadLine();
int[] arr = Array.ConvertAll(Console.ReadLine().Split(' '),int.Parse);
List<int> lis = new List<int>(){arr[0]};

for (int i = 1; i < arr.Length; i++)
{
    if(arr[i] > lis[lis.Count-1])
        lis.Add(arr[i]);

    else
        {
            int left = 0;
            int right = lis.Count -1;

            int mid = 0;

            while (true)
            {
                if(left >= right)
                    break;
                
                mid = (right + left) / 2;

                if(lis[mid] < arr[i])
                    left = mid+1;
                else
                    right = mid;
            }

            if(lis[left] >= arr[i])
                lis[left] = arr[i];
        }
}

System.Console.WriteLine(lis.Count);

 

미흡하거나 개선될수 있는 부분이 있다면 답글 남겨주세요