함수 안에서 자기 자신의 함수를 호출되는 형태를 의미
재귀를 사용함으로 복잡한 문제를 간단하게 해결할수 있다.
재귀함수는 반복적인 작업을 수행할때 반복문을 사용하는 대신 자기 자신을 호출해 문제를 해결한다.
재귀 함수는 보통 2개의 단계로 구성된다.
① 기저조건
재귀호출을 멈추는 조건을 의미
이 조건이 없다면 함수는 무한하게 호출되므로 프로그램이 정상적으로 작동되지 않는다.
② 재귀단계
자기 자신을 호출하는 부분이다.
이구간을 통해 문제의 규모를 줄여가며, 최종적으로 ① 기저조건을 만나 재귀 호출이 종료되게된다.
장점
복잡한 문제를 간결한 코드로 작성할수 있으며 반복문보다 좀더 직관적일수도 있다.
단점
호출이 많아지면 스택 오버플로우가 발생될수있음
깊은 재귀의 경우 스택 메모리사용량이 증가된다.
시각화와 추적이 어려움
재귀를 이해하기 좋은 케이스로는 피보나치 수열이 있다.

위 수열의 규칙은 1로 시작하며 arr[N] = arr[N-1] + arr[N-2] 라는 규칙을 알수있다.
배열의 각 수를 구하는 문제가 있을때, 재귀를 사용하지 않는 코드를 작성해보면
int Fibonacci(int n)
{
int[] arr = new int[n];
arr[0] = 1;
arr[1] = 1;
for (int i = 2; i < arr.Length; i++)
{
arr[i] = arr[i-2] + arr[i-1];
}
return arr[n-1];
}
System.Console.WriteLine(Fibonacci(8)); // 21
위와같은 코드가 될수도 있겠다.
재귀개념을 생각해보자.
큰 문제를 작은문제로 분할한다라고 했다.

F(5) 수열 5번의 값을 구해야할때, 위의 식처럼 표시할수 있다.
F(4) 를 좀더 작게 문제를 나눠보자. F(3) 는 나중에 해결

F(3) 를 좀더 작게 문제를 나눈다. F(2) 는 나중에 해결

F(2) 를 좀더 작게

구해야하는 값(F(5)) 로 부터 먼저 알고있는 구간 F(1) = 1 , F(0) = 0 까지 내려오게 되었다.
이 구간에서 기저조건을 만나게 해줌으로써 다시 위로 계산을 진행시킨다.
F(2) = F(1) + F(0) = 1 + 0
F(3) = F(2) + F(1) = 1 + 1
F(4) = F(3) + F(2) = 2 + 1 ...

호출 스택을 다시 거슬러 올라가보면 F(2)의 값을 어디에 저장해두지 않아서
여기서 다시 함수를 호출하게된다.
위의 과정을 다시 진행시키면,
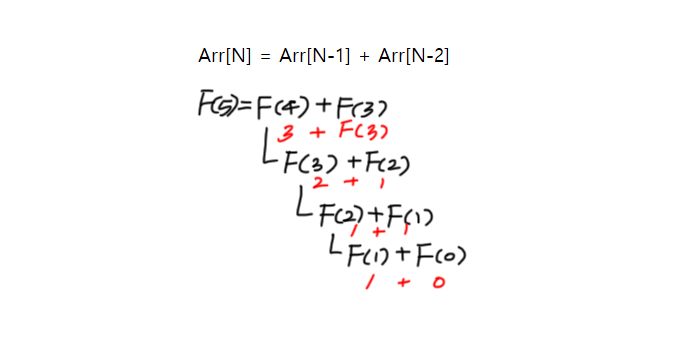
또다시 F(3)를 구하려 함수를 호출하게 될것이다.
F(3) = F(2) + F(1)
F(2) = F(1) + F(0)
이렇게 큰 문제를 작게 분할해 문제를 줄여가는 방식을 재귀라는 기법이다.
문제 https://www.acmicpc.net/problem/11729
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
점화식 아이디어
옮겨야 하는 링이 N 개일때 세워진 기둥을 각 A B C 라고 생각한다.
1(A > B) 라면 링이 한개일때 A 기둥에서 B 기둥으로 옮기는 행위라고 가정하자.
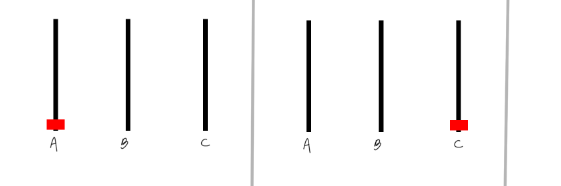
위 그림은 링 N = 1 일때 A 에서 C로 옮겨 ( 1(A > C) ) 하노이 탑을 종료하게 된다.
게임의 시작은 항상 A 라는 기둥에서 시작되며, 게임의 끝은 항상 C에 모든 링이 놓여야한다.
B는 게임에 영향을 주진 않지만 링을 잠시 보관할수 잇는 임시기둥 이라고 하자
그럼 각 기둥을 A = 시작 , B = 임시 , C = 목표 라는 명칭을 쓰도록한다.
N = 2 일때를 보자

하노이탑의 규칙대로 모든 링이 C 기둥으로 옮겨져야만 한다.
1번링이 무조건 C로 보낸다고 게임이 최소이동횟수로 끝나지 않고,
B 임시에 링을 옮겨놓고, 2번링을 C 목표에 넣어준뒤 , B 임시에 있던 링을 목표로 다시 옮겨준다.
N3 과 N4의 경우를 보자


최소이동횟수를 준수하기 위해선
① (1 ~ N-1)링을 전부 B 임시 에 옮겨준뒤
② N링을 C 목표 에 옮긴 후
③ B 임시 에 있던 링을 C 목표로 옮겨주면 된다.
다시 N2 의 그림을 보자

자세한 과정으로는
A - B 시작 > 임시
A - C N번 링을 시작 > 목표
B - C 임시 > 목표
위의 N4과정을 보면 과정이 똑같다.
이러한 특징을 가지고 재귀적으로 접근하면 되겠다.

풀이
using System.Text;
StringBuilder sb = new StringBuilder();
int input = int.Parse(Console.ReadLine());
sb.AppendLine($"{(int)(Math.Pow(2,input)-1)}");
HanoiTower(input,1,2,3);
System.Console.WriteLine(sb);
void HanoiTower(int n, int start, int temp, int target)
{
if(n <= 1)
{
sb.AppendLine($"{start} {target}");
return;
}
HanoiTower(n-1,start,target,temp);
HanoiTower(1,start,temp,target);
HanoiTower(n-1,temp,start,target);
}
미흡하거나 개선될수 있는부분이 있다면 답글 남겨주세요
'알고리즘 > 전략' 카테고리의 다른 글
| Dynamic Programming 동적 계획법 (0) | 2024.03.07 |
|---|---|
| 메모이제이션 최적화기법 (0) | 2024.03.07 |
| 그리디 (Greed) 알고리즘 (0) | 2024.03.03 |